A parallel hashed Oct-Tree N-body algorithm

Citation: Micheal S. Warren, John K. Salmon (1993/10) A parallel hashed Oct-Tree N-body algorithm. ACM/IEEE conference on Supercomputing (RSS)
DOI (original publisher): 10.1145/169627.169640
Semantic Scholar (metadata): 10.1145/169627.169640
Sci-Hub (fulltext): 10.1145/169627.169640
Internet Archive Scholar (search for fulltext): A parallel hashed Oct-Tree N-body algorithm
Download: https://dl.acm.org/doi/10.1145/169627.169640
Tagged: Computer Science (RSS) Parallel Systems (RSS), Scientific Computing (RSS)

Summary

The N-body problem requires calculating ${\mathcal {O}}(N^{2})$ body-to-body interactions to solve exactly. Instead, one can form an ${\mathcal {O}}(N\log N)$ algorithm by clustering bodies together, and considering the cluster as a single representative body, with series corrections. However, efficient implementations require an oct-tree data-structure and a novel oct-tree hashing scheme.

Theoretical and Practical Relevance

Oct-tree hashing unlocks the door for efficient N-body simulations and other problems in computational physics.

Problem

1. Simulate the N-body problem
   • "Force" can be gravitational, Coulombic, or anything else that is particle-to-particle dependent.
2. Exact solution involves $N(N-1)$ interactions. Thus, we need to use approximations.
   • Evaluate the field at every point on a grid.
     • Making the grid high-precision is expensive.
   • Group particles into hierarchical cells, treat the cells as a single bigger particle, with some truncated series corrections. Since the division is hierarchical, recurse within each cell.
     • In general, this is more accurate when the cells are smaller, other cells are far away, and the cell has smaller moments (the moment is a measure of how heavy the cell is far away from its center).
     • How to split particles to maintain precision without sacrificing speed?

Other solutions

• Appel's method: partitions particles into spherical cells, ${\mathcal {O}}(N)$.
  • Apparently B-H is slower in theory but faster in practice.
• Barnes-Hut method (B-H): partitions particles into oct-trees, ${\mathcal {O}}(N\log N)$.
  • No error bound before this paper.
  • No efficient implementation before this paper.
• Fast Multipole Method (FMM): ${\mathcal {O}}(N)$
  • Also fast in theory, slow in practice. The "crossover point" when FMM beats the naïve ${\mathcal {O}}(N^{2})$ is 70 thousand particles.

Contributions

• B-H error bound: the particle division and error bound has to be "data-dependent" or else it will be really high.
  • This paper derives such a bound.
• But if the division is data-dependent, it is difficult to know which non-local cells are required before computation.
  • Remember on supercomputers, the memory is distributed across tens of thousands of nodes. They use message-passing.
• Instead, make it easier/faster to retrieve non-local data during computation.
  • Prior work used an Oct-tree. An oct-tree is a 3-D extension of a quad-tree. In a quad-tree, each node has a 2-D coordinate. Each node has 0 or 4 children: one must lie northeast of the parent, one northwest, one southeast, and one southwest. As such, they hierarchically partition 2-D space.
  • Prior work stores this table as a pointer to a block containing child pointers and a data pointer. One has to do many pointer dereferences to get to the leaves.
  • This work turns each coordinate into a key and uses a hashtable to map keys to data. The hashing function alluded to in the title is the main-contribution of this paper.
    • The hash intertwines the digits of their coordinates and truncates the most-significant digits.
    • 
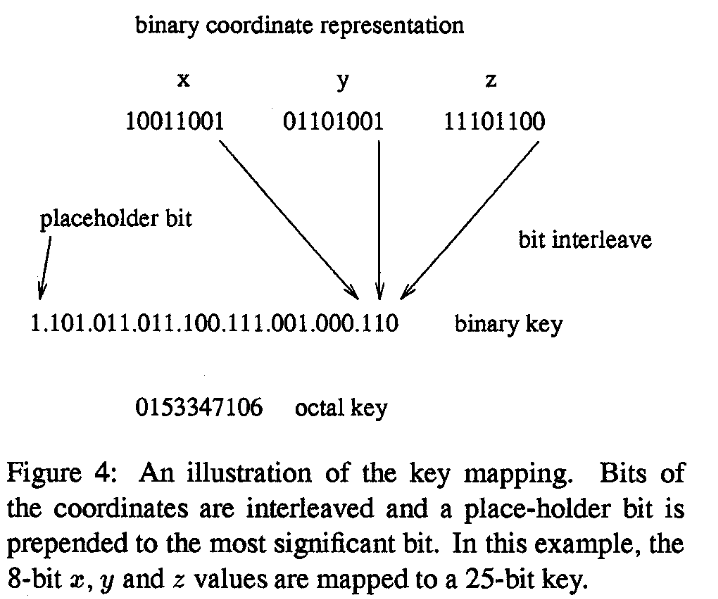
    • This way, children can access their parent, by just truncating their digits Parents can get to their children by appending some digits (appending 100 gets the upper-deck northeastern child, 001 gets the lower-deck southeastern child, etc.).
    • Hashing uses the $N$ least-significant digits, so two points with the same hash (AKA a hash-collision) will be separated by a distance of at least $2^{N}$. This the opposite of locality-sensitive hashing. This way, collisions are handled by different machines, which spreads out the load.
    • Counting up in digits iterates over every key in depth-first order. This sequence of points creates a space-filling fractal called, the Z-order curve.
    • 
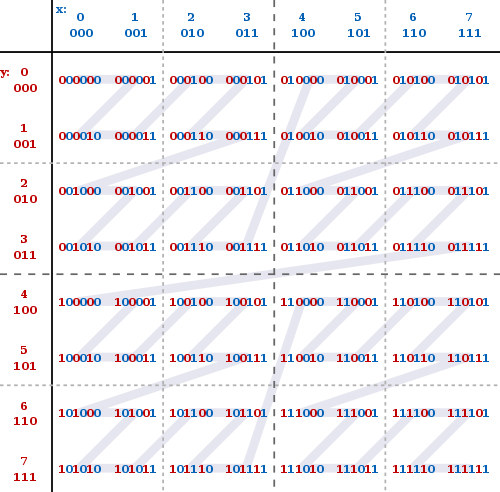
  • Care must be taken to balance the oct-tree, to have good performance. One can sort the list of keys, and cut it in halves recursively, weighted by how much work we think each node will be.
    • Unfortunately, the Z-order curve has spatial discontinuities, so two points can be close in Z-order, but be far away in space. Maybe use Hilbert curve. So one processor's allocation of cells may interact with a lot of other processors.
  • In practice, iteration in breadth-first order will hide the latency of requesting spatially-disparate children; the requests can go in parallel to (probably) different processors.
• These techniques can also be used for fluid mechanics.